Anecdotal case-studies of patients with various brain lesions have demonstrated the dissociation of different calculation elements, thereby supporting the assumption that numerical ability represents a multifactor skill, requiring the participation of different abilities and quite diverse brain areas (Ardilla and Rosselli, 2002). These case studies have also allowed for the subtyping of dyscalculia and acalculia. Mathematical and arithmetic abilities can be impaired as a result of language, spatial, or executive functions. Ardilla and Rosselli (2002) detail some of the subtypes and associated ROIs (some of which are labeled on the diagram below):
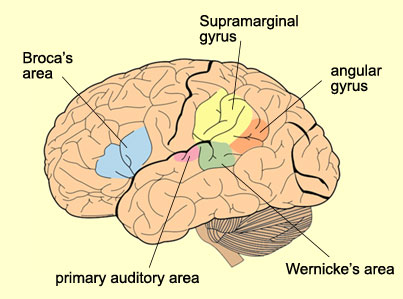
Anarithmetia could be interpreted as a defect in understanding how the numerical system works, and is associated with damage to the left angular gyrus. Damage to the left angular gyrus is also associated with Gerstmann’s syndrome, which combines dyscalculia with finger agnosia (and results in an inability to count on one’s fingers), as well as dysgraphia and right-left disorientation. When electrical stimulation is applied to the angular gyrus in otherwise normal individuals, they present with signs of Gerstmann’s syndrome.
Patients with acalculia in Broca’s aphasia present with errors in the syntax of calculation. That is, they present “stack errors” (e.g. 14 is read as 4). While counting forward is not affected, counting backward relies more on verbal sequencing, and is impaired. Errors in transcoding numbers from verbal code to numerical code are present (e.g. “three hundred and seven” to 307), as are hierarchical errors (e.g. patients do not understand the difference between the two times the word “hundred” appears in “three hundred thousand, two hundred”). As this is associated with Broca’s aphasia, it is associated with the left inferior frontal gyrus.
Patients with acalculia in Wernicke’s aphasia present semantic and lexical errors in saying, reading, and writing numbers. However, simple mental arithmetic operations are errorless. Like in Broca’s aphasia, most of the errors that present in this case are language related. As these symptoms are associated with Wernicke’s aphasia, the left posterior superior temporal gyrus is implicated.
Patients with spatial acalculia have no difficulties in counting or in performing successive operations. However, some fragmentation appears in reading numbers (e.g. 523 becomes 23), resulting from left hemi-spatial neglect. Reading complex numbers is also prone to errors, as the spatial position of each digit relative to the other digits becomes important: 1003 becomes 103, 32 becomes 23, or 734 becomes 43. When writing, patients cannot line up numbers in columns, creating difficulty in arithmetic calculation. Moreover, digit iterations are frequent (e.g. 27 becomes 22277), as are feature iterations (e.g. 3 is written with extra loops). The patient has a full understanding of “carrying over” in subtraction, but cannot find the proper location to write the number.
Patients with frontal (executive function) acalculia have damage in the pre-frontal cortex. These patients typically present with serious difficulties in mental arithmetic operations, successive operations (particularly subtraction), and solving multi-step numerical problems. They generally also have serious disturbances in applying mathematical knowledge to time (e.g. they could not tell you if America was founded closer to 10 years ago or to 200 years ago). When aided by pencil and paper, however, most of these patients are errorless.
As the quality and quantity of different types of non-invasive neuroimaging methods has increased, researchers have been able to examine different regions of interest throughout the brain to discover how they are involved in mathematics and arithmetic, and how they can be implicated in developmental dyscalculia. Dehaene et al. (2004) carried out a series of fMRI investigations, in a study called Arithmetic and the Brain. They found a set of parietal, prefrontal, and cingulate areas which were reliably activated by patients undergoing mental calculation. The precentral sulcus is often co-activated with the inferior frontal gyrus. They’ve also considered the role of the left and right fusiform gyri and occipito-temporal regions in recognizing visual number forms.
Dehaene (2004) has implicated the angular gyrus in mathematics and arithmetic. The angular gyrus has been activated by digit naming tasks as well as mental multiplication. This was demonstrated by a study in which a normal patient’s angular gyrus was electrically stimulated, which disrupted multiplication. In addition, metabolic abnormalities have been found in the angular gyrus in individuals with dyscalculia: a focal defect in a left temporo-parietal brain region near the angular gyrus was isolated, with differential decreases in N-acetyl-aspartate, creatine, and choline (Levy, Reis, and Grafman, 1999).
A region of interest that has received lots of attention in dyscalculia research is the horizontal segment of the intraparietal sulcus (HIPS), in both hemispheres. Activation of the right and left HIPS has been seen during basic calculation tasks as well as digit detection tasks. Further, is it multi-modal, responding equally to spoken words and written words, as well as Arabic numerals. Right HIPS activation has also been seen in tasks where subjects estimate the numerosity of a set of concrete visual objects. Electrical stimulation of an anterior left HIPS site disrupted subtraction. Isaacs et al. (2001) found a left IPS reduction in grey matter in children with developmental dyscalculia at the precise coordinates where activation is observed in normal children during arithmetic tasks.
Molko et al. (2003) studied individuals with Turner Syndrome, a genetic X-linked condition which is associated with abnormal development of numerical representation. In the right IPS, a decrease in maximal depth as well as a trend toward reduced length was observed for subjects with Turner Syndrome when compared with control subjects. Additionally, the center of gravity of the central sulcus showed a significant posterior displacement in Turner Syndrome patients.
Despite the relative inter-subject irregularity of cortical geometry, there are general consistencies found in normal individuals. For example, the anterior-posterior orientation of the IPS, its downward convexity, as well as its segmentation into three parts, was observed in all controls. In contrast, the right intraparietal sulcal pattern of most subjects with Turner Syndrome did not conform to those patterns due to aberrant branches, abnormal interruption, or unusual orientation. For example, the three segments were only observed in 7 of 14 Turner Syndrome subjects, while the downward convexity was only seen in 3 of 14.
In agreement with the fMRI findings of Dehaene et al. (2004), during exact and approximate calculation tasks, Molko et al. (2003) found reduced activation in the right IPS as a function of number size. Similar fMRI hypoactivations were found in a broader parieto-prefrontal network in two other genetic conditions associated with developmental dyscalculia: fragile X syndrome and velocardiofacial syndrome (Dehaene et al., 2004).
In a meta-analysis of fMRI studies of arithmetic and numbers, Dehaene offer a tripartite organization for number processing in the brain:
The horizontal segment of the intraparietal sulcus (HIPS) appears as a plausible candidate for domain specificity: It is systematically activated whenever numbers are manipulated, independently of number notation, and with increasing activation as the task puts greater emphasis on quantity processing. Depending on task demands, we speculate that this core quantity system, analogous to an internal “number line,” can be supplemented by two other circuits. A left angular gyrus area, in connection with other left-hemispheric perisylvian areas, supports the manipulation of numbers in verbal form. Finally, a bilateral posterior superior parietal system supports attentional orientation on the mental number line, just like on any other spatial dimension. (Dehaene, Piazza, Pinel, and Cohen, 2003, p.1)